报告地点:舜耕校区实验楼505会议室
报告时间:2026年1月6日(星期二)8:30—12:00
主办单位:swag做爱
协办单位:科研处,黄河流域生态统计协同创新中心、现代统计交叉科学重点实验室、统计学博士后科研流动站、中加项目管理委员会
一、 青年教师工作论文报告
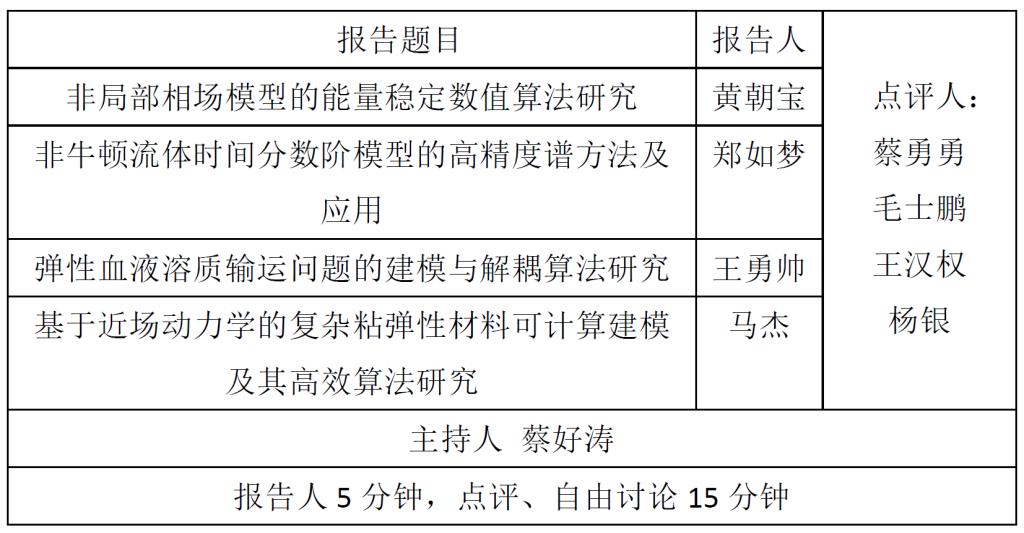
二、特邀专家报告
报告(一)
报告题目:Numerical methods and analysis for oscillatory dispersive PDEs
报告人:蔡勇勇 教授(北京师范大学)
摘要: Dispersive PDEs, such as Klein-Gordon equation, Dirac equation, Schrodinger equation, arise from many different areas, e.g. computational chemistry, plasma physics, quantum mechanics. Typical computational tasks in dispersive PDEs are finding the ground/stationary states and solving the dynamics. In this talk, we report some recent advances on the numerical methods and analysis for the time-dependent dispersive PDEs, paying particular attention to the highly oscillatory PDEs, which usually exhibit solutions with high frequency waves in time and/or in space, and are computationally expensive.
报告人简介:蔡勇勇,北京师范大学教授,本科和硕士就读于北京大学,2012年在新加坡国立大学获得博士学位。他先后在威斯康辛大学麦迪逊分校、马里兰大学帕克分校和普渡大学从事博士后研究工作,从2016年至2019年在北京计算科学研究中心任特聘研究员,2016年入选海外高层次青年人才计划。蔡勇勇博士的研究兴趣主要是偏微分方程的数值方法及其在量子力学等领域中的应用,在MCOM、JCP和SIAM系列等期刊上发表多篇论文,多次受邀参加学术会议,并在SciCADE2019和ICOSAHOM2023上作大会报告。
报告(二)
报告题目:磁流体力学的保结构和保物理有限元算法
报告人:毛士鹏 研究员(中国科学院大学)
摘要:磁流体力学研究导电流体与电磁场相互作用的运动规律,其能量定律、质量守恒、无散度磁场、电流密度守恒、螺旋度守恒等物理定律是其基本物理性质,一般在数值计算中只能近似的满足这些物理性质,如何设计精确保持这些物理性质的数值计算方法是磁流体工程计算非常重要的研究课题之一。我们针对不可压缩磁流体提出了首个能够在各自的物理极限下精确保持包括质量守恒、磁场无散度、电流密度守恒、能量守恒、磁螺旋度和流体螺旋度守恒这些关键物理属性的全离散有限元方法,并发展了支持磁流体螺旋度守恒的线性求解方案,针对保物理离散系统开发了高效健壮的磁流体预处理求解器,这些预处理器在流体和磁雷诺数较高的情况下仍具有鲁棒性。数值实验测试了所提出数值方法在极端物理参数下能够保留所有这些物理属性前提下的准确性、稳定性和鲁棒性。测试例子包括Orszag Tang涡旋和驱动磁重联的一些基准问题,流体和磁雷诺数可以同时高达10^6。
报告人简介:毛士鹏,中科院数学与系统科学研究院研究员、博士生导师,中科院大学岗位教授。2008年博士毕业于中科院数学与系统科学研究院,2008-2012先后在在法国国家信息自动化研究院(INRIA)以及在瑞士苏黎世高工(ETH Zurich)做博士后和研究助理,2012年开始在中科院数学与系统科学研究院分别任助理研究员和副研究员,研究员。主要从事有限元方法及其应用、计算流体力学和磁流体力学、自适应算法等领域的研究工作,部分工作发表在Math. Comp., Numer. Math., SINUM., SISC., M3AS, JCP, CMAME,PoF等知名刊物, 承担来自科技部,基金委,中物院等单位的10余项重要科研任务课题。
报告(三)
报告题目:数据驱动的任意多项式混沌展开式及其在不确定性量化问题中的应用
报告人:王汉权 教授(云南财经大学)
摘要:不确定性量化(Uncertainty Quantification, UQ)旨在量化随机输入或信息不完备条件下不确定性对模型输出的影响及其传播特性,在科学计算与工程分析中具有重要意义。本报告围绕多项式混沌展开式、任意多项式混沌展开式及其扩展方法在 UQ 问题中的应用,给出适用于不同场景的替代模型构建与求解方法,通过随机函数与随机薛定谔方程算例,验证所提方法的有效性与高效性。涉及到的研究对一般UQ问题的求解,特别是对含随机数据输入的随机偏微分方程的高效求解具有一般意义。
报告人简介:
王汉权,云南财经大学教授,博士生导师,中国工业与应用数学学会第九届常务理事,中国数学会计算数学分会常务理事,云南省中青年学术带头人,云南省数学学会副理事长,云南省工业与应用数学学会副理事长,云南省数学类专业教学指导委员会委员,四川大学数学学院兼职博士生导师。研究方向为计算数学与科学工程计算,各种偏微分方程、随机偏微分方程的数值解法(有限差分法、谱方法、谱元法等)的设计与应用,泛函极值问题求解方法设计与应用,最优化理论方法与应用,智能学习与计算方法,:主持过10余项省部级以上级别科学研究项目(包括主持5项国家自科基金项目)获得教育部2013年度新世纪优秀人才, 2014年7月31日;获得“云南省有突出贡献优秀专业技术人才”称号, 三等奖 ;2017年10月,获得“云南省自然科学奖”, 三等奖 2017年11月,获得“云南省中青年学术带头人”称号;
报告(四)
报告题目:Multicontinuum homogenization in perforated domain
报告人:杨银 教授(湘潭大学)
摘要:In this talk, we develop a general framework for multicontinuum homogenization in perforated domains. The simulations of problems in perforated domains are expensive and, in many applications, coarse-grid macroscopic models are developed. Many previous approaches include homogenization, multiscale finite element methods, and so on. In our paper, we propose multicontinuum homogenization method for problems in perforated domains. We distinguish different spatial regions in perforations based on their sizes. For example, very thin perforations are considered as one continuum, while larger perforations are considered as another continuum. By differentiating perforations in this way, we are able to predict flows in each of them more accurately. Cell problems are formulated for each continuum using appropriate constraints for the solution averages and their gradients. These cell problem solutions are used in a multiscale expansion and in deriving novel macroscopic systems for multicontinuum homogenization. Our proposed approaches are designed for problems without scale separation. We present numerical results for two continuum problems and demonstrate the accuracy of the proposed methods.
报告人简介:杨银,湘潭大学教授,博士生导师。现任湘潭大学数学与计算科学学院院长、湖南国家应用数学中心副主任主要从事偏微分方程高效数值方法研究。主持国家重大研究计划项目课题1项、国家自然科学基金中俄国际合作项目1项、国家自然科学基金项目4项,发表学术论文50余篇;获教育部U40计划、湖南省科技创新领军人才、湖南省杰出青年基金、宝钢优秀教师奖。

